qPCR における ΔΔCt 法を使用する際に知っておくべきすべてのこと

以下の内容は、英語の原文をもとに ChatGPT により自動翻訳されたものです。専門用語の正確さと表現の明瞭さに配慮しておりますが、参考用としてご利用ください。

ΔΔCt 法を使って qPCR 解析を行っているとき、コントロール群の平均発現量が「1 ちょうど」になっていない、という場面に出くわしたことはありませんか？そのとき、あなたはどうしましたか？黙って ΔΔCt の結果を もう一度 正規化して、コントロール群の平均を 1 に「戻そう」としたことはありませんか？そして、その「こっそりとした追加の正規化」は本当に妥当なのか、それともずっと怪しいことをしていたのではないか、疑問に思ったことはありませんか？

このブログ記事では、その疑問を徹底的に解き明かします。
この二次的な正規化は数学的に正当化できるのか？それとも、単なる完璧主義者の自己満足なのか？
さっそく、見ていきましょう。

1. qPCR の背景

定量的 PCR（qPCR、またはリアルタイム PCR）は、DNA を増幅しながら同時に定量する分子生物学的手法です。従来の PCR（ポリメラーゼ連鎖反応）を基盤としつつ、DNA の増幅をリアルタイムでモニタリングできる機能が追加されています。

🔬 1.1 基本原理

qPCR では、蛍光色素（例：SYBR Green）や 蛍光標識プローブ（例：TaqMan）を使用し、各 PCR サイクル中に生成された DNA の量に比例した蛍光を放出します。この蛍光シグナルは各サイクルごとに測定され、目的 DNA の定量を可能にします。

🧪 1.2 応用例

遺伝子発現解析（逆転写 RNA から作成された cDNA を使用）
病原体検出（例：ウイルス、細菌）
ジェノタイピングおよび突然変異解析
RNA-seq やマイクロアレイの検証

📈 1.3 主要な指標：Ct 値

サイクルしきい値（Ct 値）とは、蛍光シグナルがバックグラウンドを超えるのに必要なサイクル数のことです。Ct 値は開始時の DNA 量と逆相関しており、Ct 値が低いほど、初期 DNA 量は多いことを意味します。

2. $2^{-\Delta\Delta{C_{T}}}$ 法

この手法は、Kenneth J. Livak および Thomas D. Schmittgen により 2001 年 12 月に発表された重要な論文
“Analysis of relative gene expression data using real-time quantitative PCR and the 2(–ΔΔCT) Method” において提案されました。

Applied Biosystems（カリフォルニア州フォスターシティ）で開発されたこの手法は、リアルタイム PCR を用いた相対的遺伝子発現解析を効率化するものであり、増幅効率が等しいと仮定する場合には標準曲線が不要になります。
（参考：Guide to Performing Relative Quantitation of Gene Expression Using Real-Time Quantitative PCR）

3. 興味深い発見

元の $2^{-\Delta\Delta C_T}$ 法に対して追加で正規化（すなわち、$2^{-\Delta\Delta C_T}$ をコントロール群内の $2^{-\Delta\Delta C_T}$ の平均で割る）を行うことは、$2^{-\Delta C_T}$ をコントロール群内の $2^{-\Delta C_T}$ の平均で割ることと等価である、という結果が得られました。これは以下の Microsoft Excel ファイルのスクリーンショットで示されています：

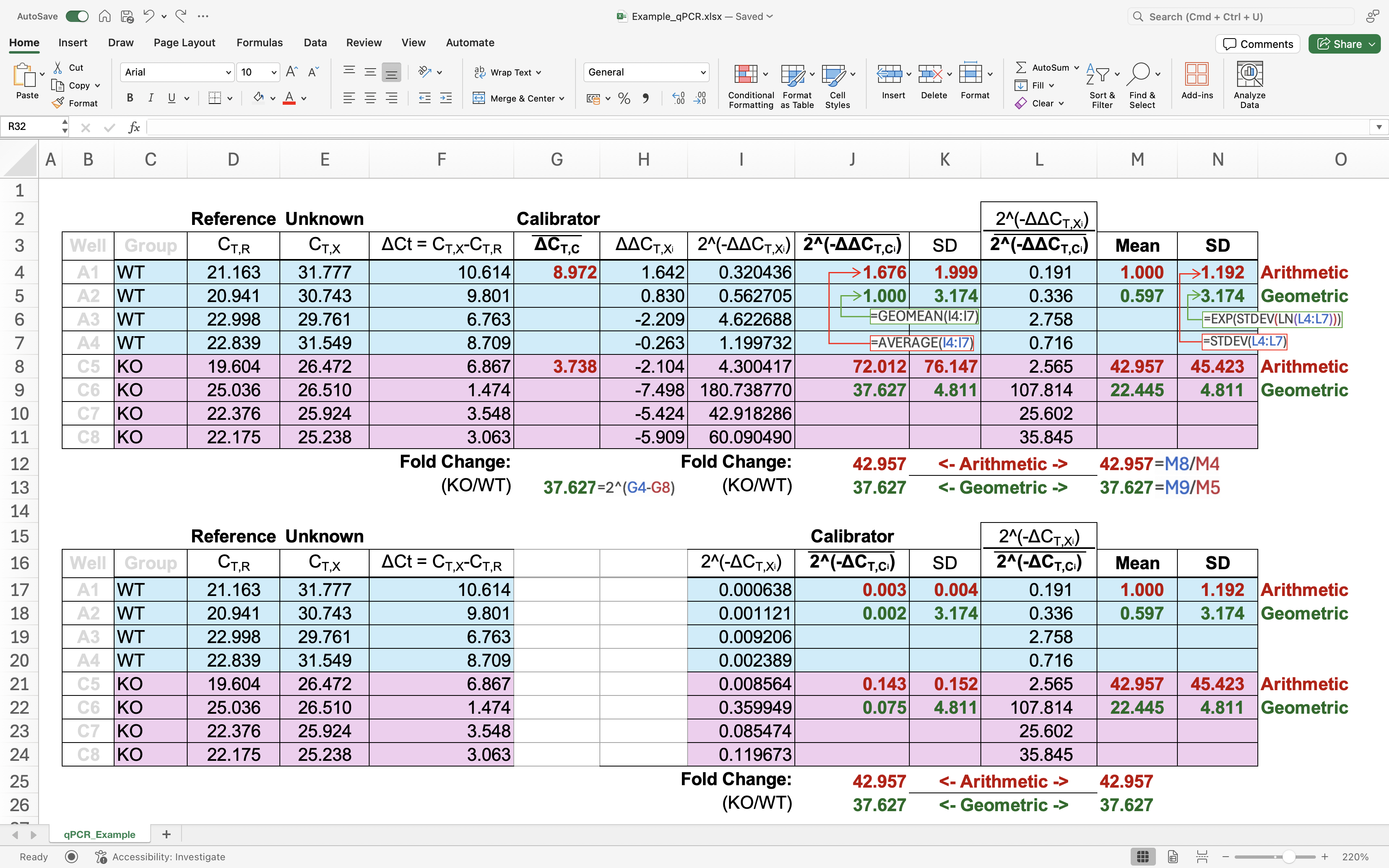Identical_qPCR_Results 図 1. 上図のように、これら 2 つの方法は同じフォールドチェンジ値を生み出します（Example_qPCR.xlsx 参照）。

この現象を理解するためには、まず使用する記号や用語を統一する必要があります。

3.1 記号の定義

以下の記号を定義します：

PCR サイクル数：$C$
PCR 効率：$E$
しきい値サイクル：下付き文字 $T$
参照遺伝子（例：ハウスキーピング遺伝子）：下付き文字 $R$
調べたい未知の遺伝子：下付き文字 $X$
クエリ群（実験群）における $X$：下付き文字 $q$
コントロール群における $X$：下付き文字 $c$
サンプルのインデックス：$i$

注：各サンプルは、対象遺伝子 $X$ と参照遺伝子 $R$ の両方を含むため、1 サンプル内でペアとして扱われます。

次に、以下の仮定と定義を行います：

$(1 + E)$ は PCR の増幅率（一般的には $\approx 2$）。単純化のため、理想的な効率すなわち $E_X = E_R = E = 1$ と仮定します。
$C_{T,R}$ はすべてのサンプルにおける参照遺伝子 $R$ のしきい値サイクル（例：GAPDH、18s、β-アクチンなど）。
$C_{T,X}$ はすべてのサンプルにおける対象遺伝子 $X$ のしきい値サイクル。
クエリ群のサンプル $i$ における $\Delta C_T$ は：
$\Delta C_{T,Q_{i}} = C_{T,X_{Q,i}} - C_{T,R_{Q,i}}$
コントロール群のサンプル $i$ における $\Delta C_T$ は：
$\Delta C_{T,C_{i}} = C_{T,X_{C,i}} - C_{T,R_{C,i}}$

Livak & Schmittgen, 2001 によれば、キャリブレーター（基準値）はコントロール群の $\Delta C_{T,X_c}$ の平均として定義されます：

\[\overline{\Delta C_{T,C}} = \frac{1}{n} \sum_{i=1}^n \Delta C_{T,C_i} \tag{1}\]

そして、以下を定義します：

$\Delta\Delta C_{T,X_i} = \Delta C_{T,X_i} - \overline{\Delta C_{T,C}}$
$\Delta\Delta C_{T,Q_i} = \Delta C_{T,Q_i} - \overline{\Delta C_{T,C}}$
$\Delta\Delta C_{T,C_i} = \Delta C_{T,C_i} - \overline{\Delta C_{T,C}}$

前述の Excel 表計算の観察を以下の式で表すことができます：

\[2^{-\Delta C_{T,X_i}}\div\overline{2^{-\Delta C_{T,C}}} = 2^{-\Delta\Delta C_{T,X_i}}\div \overline{2^{-\Delta\Delta C_{T,C}}}\tag{2}\]

ここで：

$\overline{2^{-\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}$
$\overline{2^{-\Delta\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta\Delta C_{T,C_i}}$

この式の左辺は以下の操作を示しています：各サンプルで対象遺伝子 $X$ を参照遺伝子 $R$ に正規化し、それをさらにコントロール群の $X/R$ の算術平均で正規化するという 2 段階の正規化です。

一方、右辺は元の $2^{-\Delta\Delta C_T}$ 値を、コントロール群の $2^{-\Delta\Delta C_T}$ の平均でさらに正規化する操作を示しています。

電卓ソフトでの計算結果によれば、これら 2 つの正規化方法はまったく同じ結果を生み出します。次のセクションでは、これら 2 つの方法が数学的に等価であることを示します。

3.2 式 (2) の導出

まず、式 (2) の右辺の分子部分を展開してみましょう：

$\Delta\Delta C_{T,X_i} = \Delta C_{T,X_i} - \overline{\Delta C_{T,C}} \tag{2}$ の定義より：

\[2^{-\Delta\Delta C_{T,X_i}} = 2^{-(\Delta C_{T,X_i} - \overline{\Delta C_{T,C}})} = \frac{2^{-\Delta C_{T,X_i}}}{2^{-\overline{\Delta C_{T,C}}}}\]

次に、式 (2) の右辺の分母部分を展開します：

$\overline{2^{-\Delta\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta\Delta C_{T,C_i}}$
また、$\Delta\Delta C_{T,C_i} = \Delta C_{T,C_i} - \overline{\Delta C_{T,C}}$ であるため：

\[\overline{2^{-\Delta\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-(\Delta C_{T,C_i} - \overline{\Delta C_{T,C}})} = \frac{1}{n}\sum_{i=1}^{n} \frac{2^{-\Delta C_{T,C_i}}}{2^{-\overline{\Delta C_{T,C}}}}\]

よって：

\[\frac{1}{n}\sum_{i=1}^{n} \frac{2^{-\Delta C_{T,C_i}}}{2^{-\overline{\Delta C_{T,C}}}} = \frac{\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}{n\cdot 2^{-\overline{\Delta C_{T,C}}}}\]

したがって、全体の式は以下のようになります：

\[\frac{2^{-\Delta C_{T,X_i}}}{2^{-\overline{\Delta C_{T,C}}}} \div \frac{\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}{n\cdot 2^{-\overline{\Delta C_{T,C}}}} = \frac{2^{-\Delta C_{T,X_i}}}{\cancel{2^{-\overline{\Delta C_{T,C}}}}} \div \frac{\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}{n\cdot \cancel{2^{-\overline{\Delta C_{T,C}}}}} = \frac{2^{-\Delta C_{T,X_i}}}{\frac{1}{n} \sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}\]

また、$\overline{2^{-\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}$ なので、

\[\frac{2^{-\Delta C_{T,X_i}}}{\frac{1}{n} \sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}} = \frac{2^{-\Delta C_{T,X_i}}}{\overline{2^{-\Delta C_{T,C}}}} = 2^{-\Delta C_{T,X_i}}\div\overline{2^{-\Delta C_{T,C}}} = \text{式 (2) の左辺}\]

したがって、式 (2) の左辺は、異なる式形式から出発しているにもかかわらず、右辺と代数的に等しいことがわかります。不思議に思えますよね？では、なぜこのようなことが起きるのでしょうか？なぜ $2^{-\Delta\Delta C_{T,X_i}}$ をコントロール群の平均 $2^{-\Delta\Delta C_{T,C}}$ で割ることが、$2^{-\Delta C_{T,X_i}}$ を平均 $2^{-\Delta C_{T,C}}$ で割ることと同じ値になるのでしょうか？

では、Livak & Schmittgen, 2001 の論文に立ち返って、そこの式 (8) を確認してみましょう：

\[\frac{X_{N,q}}{X_{N,cb}}=\frac{K\times(1+E)^{-\Delta C_{T,q}}}{K\times(1+E)^{-\Delta C_{T,cb}}}=(1+E)^{-\Delta\Delta C_T}\]

Livak & Schmittgen, 2001 の Fig.2 によれば、$\Delta C_{T,cb}$ はコントロール群における $\Delta C_T$ の算術平均であると説明されています。したがって、上記の式 (8) は本ブログ記事の文脈では以下のように書き換えることができます：

\[2^{-\Delta\Delta C_{T,X_i}} = \frac{2^{-\Delta C_{T,X_i}}}{2^{-\overline{\Delta C_{T,C}}}} = \frac{2^{-\Delta C_{T,X_i}}}{2^{-\frac{1}{n} \sum_{i=1}^n \Delta C_{T,C_i}}} \tag{3}\]

この部分に注目してください：$2^{-\frac{1}{n} \sum_{i=1}^n \Delta C_{T,C_i}}$
これは $2^{-\Delta C_{T,C_i}}$ の幾何平均に相当します。なぜなら：

\[2^{-\frac{1}{n}\sum_{i=1}^{n}{\Delta C_{T,C_i}}} = \sqrt[n]{2^{-\sum_{i=1}^{n}{\Delta C_{T,C_i}}}} = \sqrt[n]{2^{-\Delta C_{T,C_1}} \cdot 2^{-\Delta C_{T,C_2}} \cdot \cdots \cdot 2^{-\Delta C_{T,C_n}}} = \left(\prod^n_{i=1}{2^{-\Delta C_{T,C_i}}}\right)^{\frac{1}{n}} \tag{4}\]

したがって、式 (2) の左辺は次のように言い換えられます：

\[2^{-\Delta C_{T,X_i}}\div\overline{2^{-\Delta C_{T,C}}} = 2^{-\Delta C_{T,X_i}}\div\frac{1}{n}\sum_{i=1}^{n}{2^{-\Delta C_{T,C_i}}}\]

つまり、これは$2^{-\Delta\Delta C_T}$ の算術平均バージョンです。これを記号で表すと：

\[2^{-\Delta\Delta{C_{T,X_i}}AM} = \frac{2^{-\Delta C_{T,X_i}}}{\overline{2^{-\Delta C_{T,C}}}} = 2^{-\Delta C_{T,X_i}}\div\frac{1}{n}\sum_{i=1}^{n}{2^{-\Delta C_{T,C_i}}} \tag{5}\]

一方、式 (3) の方は論文 Livak & Schmittgen, 2001 における元の定義であり、幾何平均バージョンの $2^{-\Delta\Delta C_T}$ を表しています。本記事の中では、それを $2^{-\Delta\Delta{C_{T,X_i}}GM}$ と表記します。

これは興味深い結果です。というのも、上記の導出は以下のような関係を示しているからです：

$\frac{\cancel{Geometric\_Mean}[\text{Sample}]}{\text{Arithmetic\_Mean}[\cancel{Geometric\_Mean}[\text{Sample}]]} = \frac{\text{Sample}}{\text{Arithmetic\_Mean}[\text{Sample}]} \tag{6}$

4. 幾何平均 vs 算術平均

4.1 いつ幾何平均を使うべきか？

多くのチュートリアルや教科書では、qPCR の結果は一般的に 対数正規分布に従うとされており、t 検定や ANOVA などの統計解析の前に log₂ 変換することが推奨されています。しかし、ΔΔCt 法では、log₂ 変換はすでに数式内に組み込まれています：

\[\log_2(2^{-\Delta\Delta C_T}) = -\Delta\Delta C_T\]

つまり、私たちは本質的に ΔΔCt 値そのものを対数空間で解析していることになります。

ここで重要な問いが生じます：
もし解析が対数空間で行われているなら、要約統計量も対数スケールに従うべきでは？
特に、フォールドチェンジの平均値を報告する際に、算術平均ではなく幾何平均と幾何標準偏差を使うべきではないでしょうか？

パラメトリック検定（t検定、ANOVAなど）の原則に従えば、これらの検定は平均値に基づいています（[[#4.3.2 Quick examples]] 参照）。
そして、$\text{Arithmetic Mean}[\log_2(2^{-\Delta\Delta C_T})] = \text{Geometric Mean}[2^{-\Delta\Delta C_T}]$ であることは [[#4.1.2 📐 Proof]] で証明されているため、log₂ 変換されたデータで統計処理する場合、幾何平均と幾何標準偏差を用いて結果を報告すべきです。

4.1.2 📐 証明

値の集合を $x_i = 2^{-\Delta\Delta C_{T,i}}$ とします（$i = 1, 2, …, n$）
- このとき：
log 変換された値の算術平均：
\[\frac{1}{n} \sum_{i=1}^{n} \log_2(x_i) = \log_2\left( \prod_{i=1}^{n} x_i^{1/n} \right) = \log_2\left(\text{Geometric Mean}[x_i]\right)\]
両辺に $2$ をべき乗として適用すると：
$2^{\text{Arithmetic Mean}[\log_2(x_i)]} = \text{Geometric Mean}[x_i]$

よって：
$\boxed{\text{Geometric Mean}[2^{-\Delta\Delta C_T}] = 2^{\text{Arithmetic Mean}[-\Delta\Delta C_T]}}$

つまり：
$\boxed{\text{Arithmetic Mean}[\log_2(2^{-\Delta\Delta C_T})] =\log_2\left(\text{Geometric Mean}[2^{-\Delta\Delta C_T}]\right)}$

実際に、先ほどの導出でも示した通り、Livak & Schmittgen (2001) の論文では、コントロール群における $\Delta C_T$ 値の算術平均を用いてキャリブレーターを求めています。これは数学的には、正規化された発現値 ($2^{-\Delta C_T}$) の幾何平均を求めていることと等価です（本記事の 式 (4) 参照）。
しかし、コントロール群と実験群間の発現フォールドチェンジは、算術平均によって暗黙的に定義されています（論文の Fig.2 を参照）。なぜでしょうか？

4.2 元論文でフォールドチェンジに算術平均を使った理由

ここまでで、ΔΔCt 法が本質的に対数空間での演算を含むことは明らかです。それにも関わらず、最終的なフォールドチェンジ値（$2^{-\Delta\Delta C_T}$）は算術平均で平均化されています。これは一見矛盾しているように思えます。ですが、ここで重要な点があります：

👉 Livak および Schmittgen (2001) の論文自身が、この選択の理由を示しています
それは「セクション3：リアルタイムPCRデータの統計解析」に記載されています。

4.2.3 彼らの発見とは？

セクション 3 において、著者たちは同一の cDNA に対して 96 回の qPCR を繰り返し実施し、データの要約方法を 2 通り示しました：

指標	平均 ± SD	変動係数 (CV)
生の $C_T$ 値	$20.0 \pm 0.194$	約 0.97%
線形変換後の $2^{-C_T}$ 値	$9.08 \times 10^{-7} \pm 1.33 \times 10^{-7}$	約 13.5%

注：生の $C_T$ 値の算術平均は、線形変換された $2^{-C_T}$ の幾何平均に等しいことが、[[#4.1.2 📐 証明]] でも示されています。

この実験から得られた重要な教訓：

❗ $C_T$ 値は対数スケールの変数であるため、直接 SD を求めると変動が過小評価される。

指数変換（$2^{-C_T}$）を行うことで、増幅シグナルにおける実際のばらつきがより正確に反映され、
この性質は $\Delta C_T$ および $\Delta\Delta C_T$ にも受け継がれます。

まとめると：

$2^{-\Delta\Delta C_T}$ の算術平均は、幾何平均（または $\Delta\Delta C_T$ の算術平均）よりもばらつきを適切に示す手法である。

このように、算術平均の使用には統計的に正当な理由があるのです。
特に、線形スケールでの発現値（$2^{-\Delta C_T}$ や $2^{-\Delta\Delta C_T}$）が正規分布に近い場合には、算術平均による解析は合理的です。

では、次の問いが浮かびます：
$2^{-\Delta C_T}$ や $2^{-\Delta\Delta C_T}$ が変動をより正確に反映するとわかっているのなら、キャリブレーターもその算術平均で定義すればよいのでは？

答えは：YES！可能です！

4.3 2つの手法はほぼ等価である

なぜでしょうか？
それは、統計的仮説検定（t検定、ANOVA、またはノンパラメトリック検定の Wilcoxon など）を実行すると、どちらの手法でも $P$ 値がまったく同じになるからです。

4.3.2 クイックな例：

t検定 はグループ間の平均値を比較します：
- 元の t検定の式：
\[t = \frac{\overline{x}_1 - \overline{x}_2}{s_p \cdot \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\]
- すべてのデータを定数 $c$ で割った場合：
\[\text{New } t = \frac{\frac{\bar{x}_1}{c} - \frac{\bar{x}_2}{c}}{\frac{s_p}{c} \cdot \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} = \frac{1}{c} \cdot \text{分子} \div \frac{1}{c} \cdot \text{分母} = \text{元の } t \text{ と同じ}\]
ここで $x$ は ΔΔCt または変換後の値（例：$2^{-\Delta\Delta C_T}$）とし、$c$ はコントロール群の $2^{-\Delta\Delta C_T}$ の算術平均とします。このとき、New $t$ は $2^{-\Delta\Delta C_T}$ の算術平均バージョンを使ったものですが、最終的な $t$ 値は変わらず、$P$ 値も同じになります。
ANOVA は総分散を分割し、グループ間の平均値を比較します。F統計量は一様なスケーリングに対して不変です：
\[F = \frac{\text{グループ間分散}}{\text{グループ内分散}} \rightarrow \text{変化なし}\]
F統計量は分散の比率であるため、すべてのデータを定数 $c$ でスケーリングした場合、
分子・分母ともに $c^2$ が掛かるため打ち消し合います。
Wilcoxon / Mann–Whitney 検定は、順位（ランク）に基づく検定であり、単調変換に対して不変です。
つまり、算術平均や幾何平均による正規化を行っても、順位が変わらなければ検定結果は変わりません。

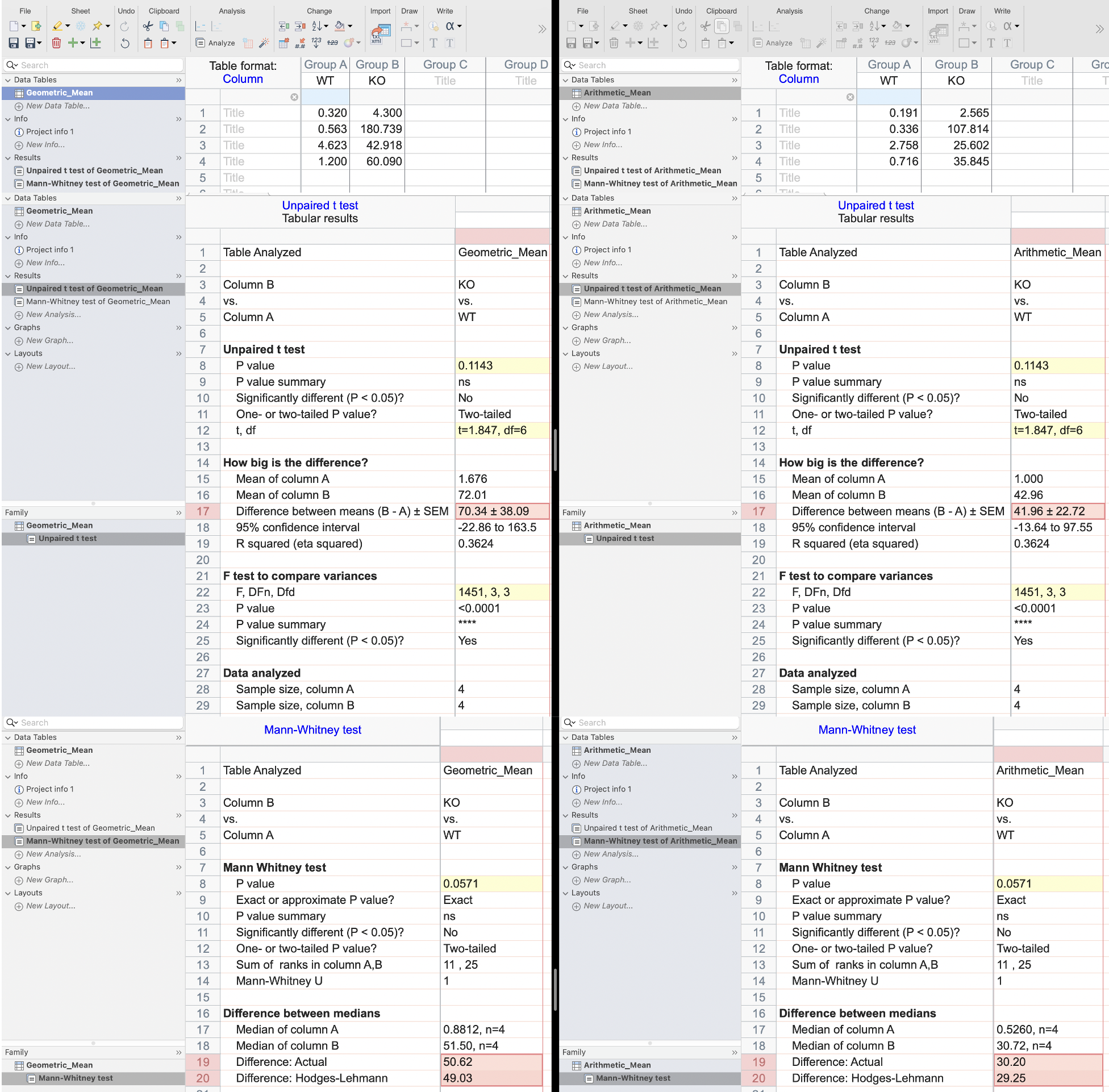
Identical_qPCR_Results

図 2. GraphPad Prism による出力結果では、正規化方法が異なっても、統計的指標（例：P 値、F、t など）はまったく同じであることが示されています(GM_Calibrator_2DDCt.prism and AM_Calibrator_2DDCt.prism)。ただし、グループ間の実際の差（例：A–B）は同一ではありません。
これは、ΔΔCt 法が相対定量に基づいているため、データの線形スケーリングを行ってもフォールドチェンジ値は変化しないという理由からです（本記事の図1 参照）。

4.4 どちらでも問題ない

ここまで数学的な細部を見てきましたが、現実世界の研究では、どちらの正規化戦略も妥当であるということが実証されています。
実際の研究現場では、ΔΔCt 法は厳密な定量のためというよりも、変化の方向性や有意性を確認するための手法として使用されることがほとんどです。

つまり、フォールドチェンジが 3.4 倍か 3.7 倍かは重要ではなく、
その変化が統計的に有意であり、生物学的に意味のあるものであるかどうかが重要です。
この意味で、ΔΔCt 法は一貫して「半定量的」または「方向性重視」であり、厳密な「定量法」ではないのです。

Livak および Schmittgen の 2001 年の論文が発表されて以来、何千もの研究—臨床試験や創薬パイプラインも含め—が $2^{-\Delta\Delta C_T}$ を用いており、その中には算術平均と幾何平均の両方を混在させて使用しているものもあります。

そして何が起こったかというと？
科学は壊れなかったのです。
研究結果は依然として正しく、薬剤候補は臨床に進み、診断マーカーも確立されました。

なぜでしょうか？

それは、正規化方法によって導入される差（例えば SD のスケーリングなど）は通常ごくわずかであり、特にあなたの研究が技術的および生物学的なリプリケートを含んでいればなおさらです。
なぜなら、qPCR の結果における標準偏差（SD）に最も影響を与えるのは、正規化方法ではなく、以下のようなシステムの性質だからです：

使用機器の性能
qPCR 試薬の品質
遺伝子配列の特性
使用している細胞や生物の生物学的多様性

言い換えれば、$2^{-\Delta\Delta C_T}$ の正規化手法によって生じる誤差は、これら上流の要因に比べて非常に小さいのです。

ですから、もし ΔΔCt 正規化の後にコントロール群の平均が「1」になっていなかったとしても、
「余分な正規化ステップで修正したい…」と思っても、心配は無用です。

幾何平均による正規化でも、算術平均による再スケーリングでも、どちらの方法も数学的に妥当であり、実証的にも安全なのです。

🧾 最終まとめ：完璧であることより、透明性が大切

では、私たちは何を学んだのでしょうか？

数学的には、$2^{-\Delta\Delta C_T}$ をコントロール群の平均（算術または幾何平均）で正規化することは、同等の結果をもたらします。これは裏技ではなく、対数変換されたデータと指数演算の代数的性質によるものです。
Livak & Schmittgen（2001）による元の ΔΔCt 法では、キャリブレーターの定義にΔCt の算術平均（= 幾何平均に相当）を使用しています。しかし、フォールドチェンジの提示には線形空間での算術平均を使用しており、これは現実的なばらつきに基づく正当化により説明されています。
ΔΔCt 値に対して統計検定（t検定、ANOVAなど）を行う場合、それらはlog 空間での演算となるため、正規化方法の有無にかかわらず、P 値・t 値・F 値は変化しません。
最も重要なのは、フォールドチェンジは変わらず、標準偏差（SD）の差もごくわずかであるという点です。特に、技術的および生物学的リプリケートが適切に設計されていれば、その差はさらに小さくなります。