Everything you shall know when using ΔΔCt method in qPCR

🌐 Other languages: English 日本語

Have you ever run into this situation while using the ΔΔCt method for qPCR analysis—your control group’s mean expression value isn’t exactly 1? What did you do? Did you quietly normalize the ΔΔCt results again just to force the control group’s mean back to 1? And have you ever wondered whether this “sneaky extra normalization” is actually valid, or if you’ve been doing something questionable all along?

Well, in this blog post, we’re going to get to the bottom of it—is this secondary normalization mathematically justified, or is it just a placebo for our inner perfectionist? Let’s find out.

1. Background of qPCR

Quantitative PCR (qPCR), also known as real-time PCR, is a molecular biology technique used to amplify and quantify DNA simultaneously. It builds upon traditional PCR (polymerase chain reaction) but adds the ability to monitor DNA amplification in real time.

🔬 1.1 Core Principle

qPCR uses fluorescent dyes (e.g., SYBR Green) or fluorescent-labeled probes (e.g., TaqMan) that emit fluorescence proportional to the amount of DNA produced during each PCR cycle. The fluorescence is measured at each cycle, enabling quantification of the target DNA.

🧪 1.2 Applications

Gene expression analysis (using cDNA from reverse-transcribed RNA)
Pathogen detection (e.g., viruses, bacteria)
Genotyping and mutation analysis
Validation of RNA-seq and microarray results

📈 1.3 Key Metric: Ct Value

The cycle threshold (Ct) is the number of cycles required for the fluorescent signal to exceed background. It inversely correlates with the amount of starting template: the lower the Ct, the higher the initial DNA quantity.

2. The $2^{-\Delta\Delta{C_{T}}}$ Method

The method was introduced by Kenneth J. Livak and Thomas D. Schmittgen in December 2001, in their pivotal paper titled “Analysis of relative gene expression data using real-time quantitative PCR and the 2(–ΔΔCT) Method”.

Developed at Applied Biosystems (Foster City, CA), it offers a streamlined approach for relative gene expression analysis using real-time PCR, eliminating the need for standard curves when amplification efficiencies are assumed to be identical (Guide to Performing Relative Quantitation of Gene Expression Using Real-Time Quantitative PCR).

3. An interesting finding

An additional normalization on the original $2^{-\Delta\Delta C_T}$ method (divide the $2^{-\Delta\Delta C_T}$ by mean of $2^{-\Delta\Delta C_T}$ in control group) is qual to dividing the $2^{-\Delta C_T}$ by mean of $2^{-\Delta C_T}$ in control group. As shown in a screenshot of a MS Excel file:

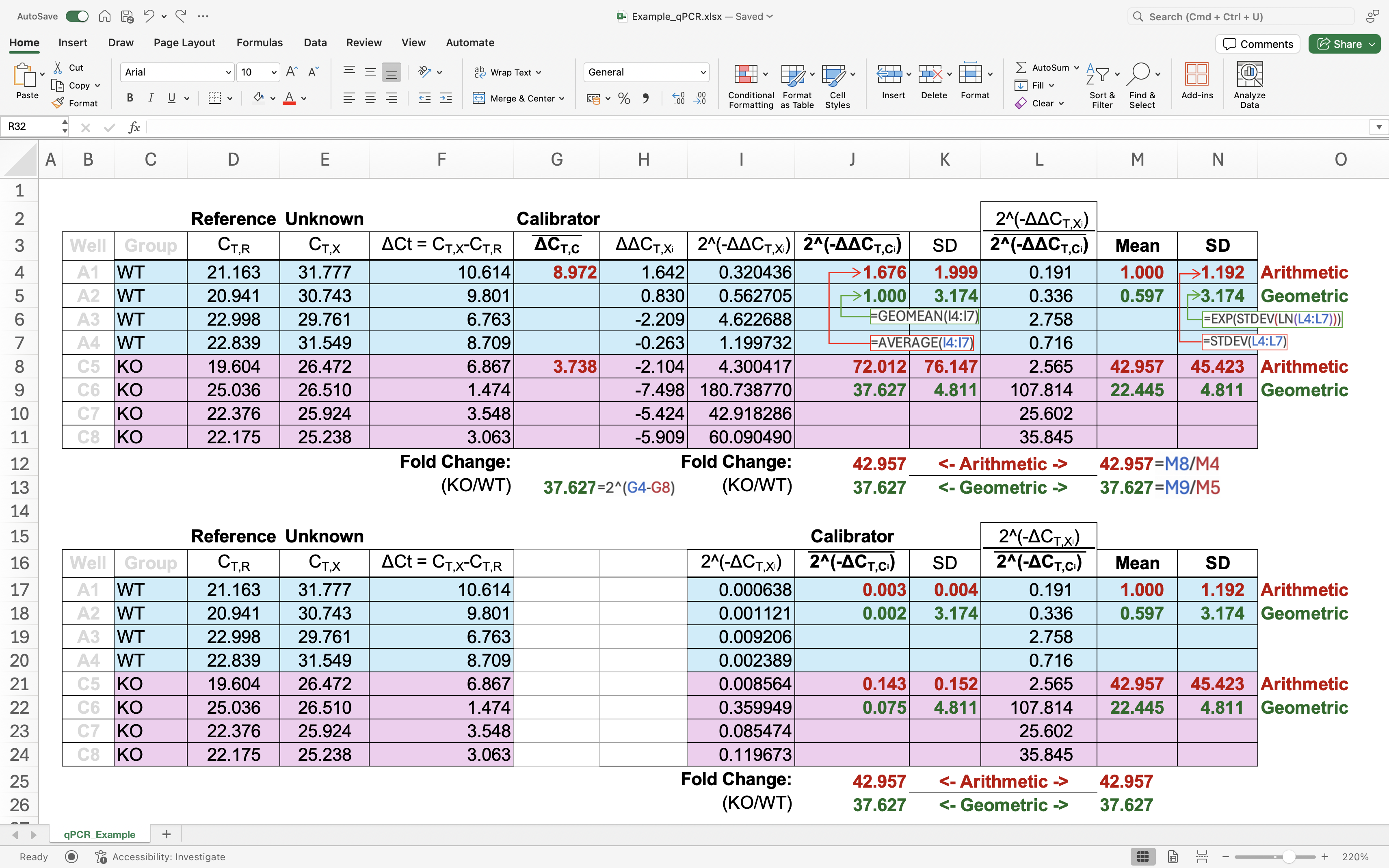Identical_qPCR_Results Figure 1. As shown in above, these two methods even yield identical fold-changes(Example_qPCR.xlsx).

To figure it out, we need to uniform our language first by define some notations.

3.1 Define notations

Let’s denote the following terms:

The PCR Cycles: $C$
The PCR Efficiency: $E$
The PCR Cycles at the threshold: subscript $T$
The Reference gene (i.e., hosekeeping gene): subscript $R$
The target interested unknown gene: subscript $X$
The target interested unknown gene ($X$) in query group: subscript $q$
The target interested unknown gene ($X$) in control group: subscript $c$
The sample index: $i$

note: Each sample contains both the target gene $X$ and the reference gene $R$, hence they are considered paired within each sample.

Then, we make the following assumptions and definitions:

$(1 + E)$ is the PCR amplification base (often $\approx2$). For simplicity, we assume ideal efficiency, i.e., $E_X = E_R = E = 1$.
$C_{T,R}$ is the Threshold Cycle ($C_{T}$) for the reference ($R$) gene in all samples (e.g., GAPDH, 18s, Beta-actin, etc.).
$C_{T,X}$ is the Threshold Cycle ($C_{T}$) for our interested unknown gene $X$ in all samples.
The $\Delta C_T$ for the query sample $i$ is defined as: $\Delta C_{T,Q_{i}} = C_{T,X_{Q,i}} - C_{T,R_{Q,i}}$
The $\Delta C_T$ for the control sample $i$ is defined as: $\Delta C_{T,C_{i}} = C_{T,X_{C,i}} - C_{T,R_{C,i}}$

According to Livak & Schmittgen, 2001, the calibrator was estimated by the mean $\Delta C_{T,X_c}$ of the control ($c$) group: $\overline{\Delta C_{T,C}} = \frac{1}{n} \sum_{i=1}^n \Delta C_{T,C_i} \tag{1}$ Then, we can define:

$\Delta\Delta C_{T,X_i} = \Delta C_{T,X_i} - \overline{\Delta C_{T,C}}$
$\Delta\Delta C_{T,Q_i} = \Delta C_{T,Q_i} - \overline{\Delta C_{T,C}}$
$\Delta\Delta C_{T,C_i} = \Delta C_{T,C_i} - \overline{\Delta C_{T,C}}$

Then, we can express the observation from the previous electric spreadsheet using the following equation: $2^{-\Delta C_{T,X_i}}\div\overline{2^{-\Delta C_{T,C}}} = 2^{-\Delta\Delta C_{T,X_i}}\div \overline{2^{-\Delta\Delta C_{T,C}}}\tag{2}$ Where:

$\overline{2^{-\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}$
$\overline{2^{-\Delta\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta\Delta C_{T,C_i}}$

The left-hand side of Equation (2) describes a normalization process: first, the target gene expression ($X$) is normalized to the reference gene ($R$) within each sample; second, these normalized values are further normalized by the arithmetic mean of the control group’s $X/R$ values.

The right-hand side of Equation (2) describes an additional normalization on the original $2^{-\Delta\Delta C_T}$ method: each $2^{-\Delta\Delta C_T}$ value is additionally normalized by the mean of the control group’s $2^{-\Delta\Delta C_T}$ values.

What we found in our calculation inside the electric spreadsheet is that these two normalization methods yield exactly the same results. In the following section, we will demonstrate that these two approaches are mathematically equivalent.

3.2 Derivation of Eq.(2)

Let’s first expand the upper part (numerator) of the right side of eq.(2):

From the definition of $\Delta\Delta C_{T,X_i} = \Delta C_{T,X_i} - \overline{\Delta C_{T,C}} \tag{2}$ , we get: $2^{-\Delta\Delta C_{T,X_i}} = 2^{-(\Delta C_{T,X_i} - \overline{\Delta C_{T,C}})} = \frac{2^{-\Delta C_{T,X_i}}}{2^{-\overline{\Delta C_{T,C}}}}$

Then, let’s expand the lower part (denominator) of the right side of eq.(1):

Because of $\overline{2^{-\Delta\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta\Delta C_{T,Ci}}$ and $\Delta\Delta C_{T,C_i} = \Delta C_{T,C_i} - \overline{\Delta C_{T,C}}$: $\overline{2^{-\Delta\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta\Delta C_{T,Ci}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-(\Delta C_{T,C_i} - \overline{\Delta C_{T,C}})} = \frac{1}{n}\sum_{i=1}^{n} \frac{2^{-\Delta C_{T,C_i}}}{2^{-\overline{\Delta C_{T,C}}}}$
Therefore: $\frac{1}{n}\sum_{i=1}^{n} \frac{2^{-\Delta C_{T,C_i}}}{2^{-\overline{\Delta C_{T,C}}}} = \frac{\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}{n\cdot 2^{-\overline{\Delta C_{T,C}}}}$

So the full expression becomes:

\[\frac{2^{-\Delta C_{T,X_i}}}{2^{-\overline{\Delta C_{T,C}}}} \div \frac{\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}{n\cdot 2^{-\overline{\Delta C_{T,C}}}} = \frac{2^{-\Delta C_{T,X_i}}}{\cancel{2^{-\overline{\Delta C_{T,C}}}}} \div \frac{\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}{n\cdot \cancel{2^{-\overline{\Delta C_{T,C}}}}} = \frac{2^{-\Delta C_{T,X_i}}}{\frac{1}{n} \sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}}\]

Because of $\overline{2^{-\Delta C_{T,C}}} = \frac{1}{n}\sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}$ , we get: $\frac{2^{-\Delta C_{T,X_i}}}{\frac{1}{n} \sum_{i=1}^{n} 2^{-\Delta C_{T,C_i}}} = \frac{2^{-\Delta C_{T,X_i}}}{\overline{2^{-\Delta C_{T,C}}}} = 2^{-\Delta C_{T,X_i}}\div\overline{2^{-\Delta C_{T,C}}} = left\ side\ of\ eq.(2)$

Hence, the left-hand side of equation (2) is algebraically equal to its right-hand side, even though they originate from different forms. looks wired, right? Then what happened in here? Why do we divide the $2^{-\Delta\Delta C_{T,X_i}}$ by the averaged $2^{-\Delta\Delta C_{T,C}}$ of control group results in the exact value as the same as when we divide the $2^{-\Delta C_{T,X_i}}$ by the average $2^{-\Delta C_{T,C}}$ ?

OK, let’s go back to the paper of Livak & Schmittgen, 2001 and check the its ref[Livak & Schmittgen, 2001].eq.(8): $\frac{X_{N,q}}{X_{N,cb}}=\frac{K\times(1+E)^{-\Delta C_{T,q}}}{K\times(1+E)^{-\Delta C_{T,cb}}}=(1+E)^{-\Delta\Delta C_T}$ According to the FIG.2 of Livak & Schmittgen, 2001, the $\Delta C_{T,cb}$ is the arithmetic mean of the $\Delta C_{T}$ in the control group. Therefore, the above ref[Livak & Schmittgen, 2001].eq.(8) can be re-written as the below equation in the context of this blog:

\[2^{-\Delta\Delta C_{T,X_i}} = \frac{2^{-\Delta C_{T,X_i}}}{2^{-\overline{\Delta C_{T,C}}}} = {2^{-\Delta C_{T,X_i}}}\div{2^{-\frac{1}{n} \sum_{i=1}^n \Delta C_{T,C_i}}} \tag{3}\]

Have you noticed this part, ${2^{-\frac{1}{n} \sum_{i=1}^n \Delta C_{T,C_i}}}$ ? This is the geometric mean of $2^{-\Delta C_{T,C_i}}$, because:

\[{2^{-\frac{1}{n}\sum_{i=1}^{n}{\Delta C_{T,C_i}}}} = \sqrt[n]{2^{-\sum_{i=1}^{n}{\Delta C_{T,Ci}}}} = \sqrt[n]{2^{-\Delta C_{T, C_1}}\cdot2^{-\Delta C_{T, C_2}}\cdot 2^{-\Delta C_{T, C_3}}...2^{-\Delta C_{T, C_n}}} = (\prod^n_{i=1}{2^{-\Delta C_{T,C_i}}})^\frac{1}{n} \tag{4}\]

Therefore, the left side of eq.(2) is actually equal to: $2^{-\Delta C_{T,X_i}}\div\overline{2^{-\Delta C_{T,C}}} = 2^{-\Delta C_{T,X_i}}\div\frac{1}{n}\sum_{i=1}^{n}{2^{-\Delta C_{T,C_i}}}$

Now, the story is totally clear, the left side of eq.(2) is the Arithmetic Mean version of $2^{-\Delta\Delta C_T}$. Let’s denote it as: $2^{-\Delta\Delta{C_{T,X_i}}AM} = \frac{2^{-\Delta C_{T,X_i}}}{\overline{2^{-\Delta C_{T,C}}}} = 2^{-\Delta C_{T,X_i}}\div\frac{1}{n}\sum_{i=1}^{n}{2^{-\Delta C_{T,C_i}}} \tag{5}$ Now, we can take the eq.(3) as the Geometric Mean of $2^{-\Delta\Delta C_T}$, which is the original in the paper of Livak & Schmittgen, 2001. For distinguish and convenience in this blog, let’s denote it as $2^{-\Delta\Delta{C_{T,X_i}}GM}$.

This is interesting, because our above steps show something like below: $\frac{\cancel{Geometric\_Mean}[Sample]}{Arithmetic\_Mean[\cancel{Geometric\_Mean}[Sample]]} = \frac{Sample}{Arithmetic\_Mean[Sample]} \tag{6}$

4. Geometric mean vs Arithmetic mean

4.1 When shall we use geometric mean for reporting

Many tutorials and textbooks state that qPCR results often follow a log-normal distribution, and therefore recommend applying a log₂ transformation (e.g., for t-tests or ANOVA). However, when using the ΔΔCt method, the log₂ transformation is already embedded in the calculation:

\[\log_2(2^{-\Delta\Delta C_T}) = -\Delta\Delta C_T\]

In other words, we are essentially analyzing ΔΔCt values directly in the log space.

This raises a key question: If our analysis is done in log space, shouldn’t the summary statistics also respect the log scale? Specifically, when we report mean fold changes, shouldn’t we use the geometric mean and geometric standard deviation, rather than the arithmetic ones?

According to the principle of parameter test (e.g., t-test, ANOVA, etc.), those tests are based on the mean of your data (see [[#4.3.2 Quick examples]]). Since $\text{Arithmetic Mean}[\log_2(2^{-\Delta\Delta C_T})] = \text{Geometric Mean}[2^{-\Delta\Delta C_T}]$ (as proofed in [[#4.1.2 📐 Proof]]), when you use log2 tranformed data for statistics, you defiantly need to use geometric mean and geometric standard deviation for reporting your results.

4.1.2 📐 Proof

Let a set of values be: $x_i = 2^{-\Delta\Delta C_{T,i}}, \quad \text{for } i = 1, 2, …, n$
- Then: Arithmetic mean of log-transformed values: $\frac{1}{n} \sum_{i=1}^{n} \log_2(x_i) = \log_2\left( \prod_{i=1}^{n} x_i^{1/n} \right) = \log_2\left(\text{Geometric Mean}[x_i]\right)$
  
  Taking base-2 exponent on both sides: $2^{\text{Arithmetic Mean}[\log_2(x_i)]} = \text{Geometric Mean}[x_i]$
  
  So: $\boxed{\text{Geometric Mean}[2^{-\Delta\Delta C_T}] = 2^{\text{Arithmetic Mean}[-\Delta\Delta C_T]}}$
  
  And therefore: $\boxed{\text{Arithmetic Mean}[\log_2(2^{-\Delta\Delta C_T})] =\log_2\left(\text{Geometric Mean}[2^{-\Delta\Delta C_T}]\right)}$

In fact, as shown in our derivation earlier, the original Livak & Schmittgen (2001) paper used the arithmetic mean of ΔCₜ values in the control group to compute the calibrator ΔCₜ. Mathematically, this is equivalent to computing the geometric mean of the normalized expression values ($2^{-\Delta C_T}$) (see eq.4 in this post). However, the fold change of expression in the control vs experiment groups is implicitly defined via arithmetic averaging in their FIG.2. Why?

4.2 Why arithmetic mean for fold-change in the original $2^{-\Delta\Delta C_T}$?

So far, we’ve established that the ΔΔCt method inherently involves log-space arithmetic, yet the final fold-change values ($2^{-\Delta\Delta C_T}$) are averaged using the arithmetic mean—a decision that seems at odds with the log-normal nature of qPCR data. But here’s the twist:

👉 Livak and Schmittgen (2001) themselves demonstrated why they made this choice—and it’s hiding in Section 3: “Statistical Analysis of Real-Time PCR Data”.

4.2.3 What they found?

In Section 3, the authors performed 96 replicate qPCR reactions on the same cDNA and reported two ways to summarize the data:

Metric	Mean ± SD	Coefficient of Variation (CV)
Raw $C_T$ values	$20.0 \pm 0.194$	~0.97%
Linear-transformed $2^{-C_T}$	$9.08 \times 10^{-7} \pm 1.33 \times 10^{-7}$	~13.5%

note: the arithmetic mean of Raw $C_T$ values is actually equal to the geometric mean of Liner-transformed $2^{-C_T}$, as we shown in the [[#4.1.2 📐 Proof]].

This experiment highlights a critical point:

❗ $C_T$ values are log-scale variables. Calculating standard deviation directly on them underestimates variability.

The exponential transformation ($2^{-C_T}$) more accurately reflects the true dispersion in the amplification signal—and this carries over to $\Delta C_T$ and $\Delta\Delta C_T$.

In short:

Arithmetic mean of $2^{-\Delta\Delta C_T}$ is better than Geometric mean of $2^{-\Delta\Delta C_T}$ (equal to arithmetic mean of $\Delta\Delta C_T$) on presenting the variabilitis.

That’s why is a a valid statistical justification for using the arithmetic mean—especially when the linearized expression values ($2^{-\Delta C_T}$ or $2^{-\Delta\Delta C_T}$) are themselves approximately normally distributed.

So the question arises:
**If we believe $2^{-\Delta C_T}$ or $2^{-\Delta\Delta C_T}$ better reflects variation, why don’t we define the calibrator using its arithmetic mean in the first place? Then, the answer is: YES! You can!

4.3 Two methods are almost equivalence

Why? Because of that when you perform statistical hypothesis tests (t-test, ANOVA, or even non-parametric tests like Wilcoxon), the $P$-values from both methods are identical.

4.3.2 Quick examples:

t-test compares group means:
- Original t-test: $t = \frac{\overline{x}_1 - \overline{x}_2}{s_p \cdot \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$
- After dividing all data by $c$: $\text{New}\ t=\frac{\frac{\bar{x_1}}{c}-\frac{\bar{x_2}}{c}}{\frac{s_p}{c}\cdot\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}= \frac{\frac{\bar{x}_1}{c} - \frac{\bar{x}_2}{c}}{\frac{s_p}{c} \cdot \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} = \frac{1}{c} \cdot \text{Numerator} \div \frac{1}{c} \cdot \text{Denominator} = \text{Same}\ t$
  
  where $x$ is ΔΔCt or any transformed version. Scaling or shifting the values (like subtracting a group mean) cancels out in the numerator and denominator. For example, let’s say $x$ is $2^{-\Delta\Delta C_T}$ and $c$ is the arithmetic mean of $2^{-\Delta\Delta C_T}$ in control group. Then, the New $t$ in the above is actually calculated from the Arithmetic Mean version of $2^{-\Delta\Delta C_T}$, the $t$ is finally the same, therefore the $P$-value is also the same.
ANOVA partitions total variance and compares group means. The F-statistic is scale-invariant under uniform normalization. The F-statistic in ANOVA is a ratio of variances, so scaling all data by a constant ccc scales both the numerator and denominator of the F-statistic by $c^2$, which cancels out: $F = \frac{\text{Between-group variance}}{\text{Within-group variance}} \rightarrow \text{unchanged} ]$
Wilcoxon/Mann–Whitney tests are based on rank order, and are invariant under monotonic transformations, including normalization by any mean.

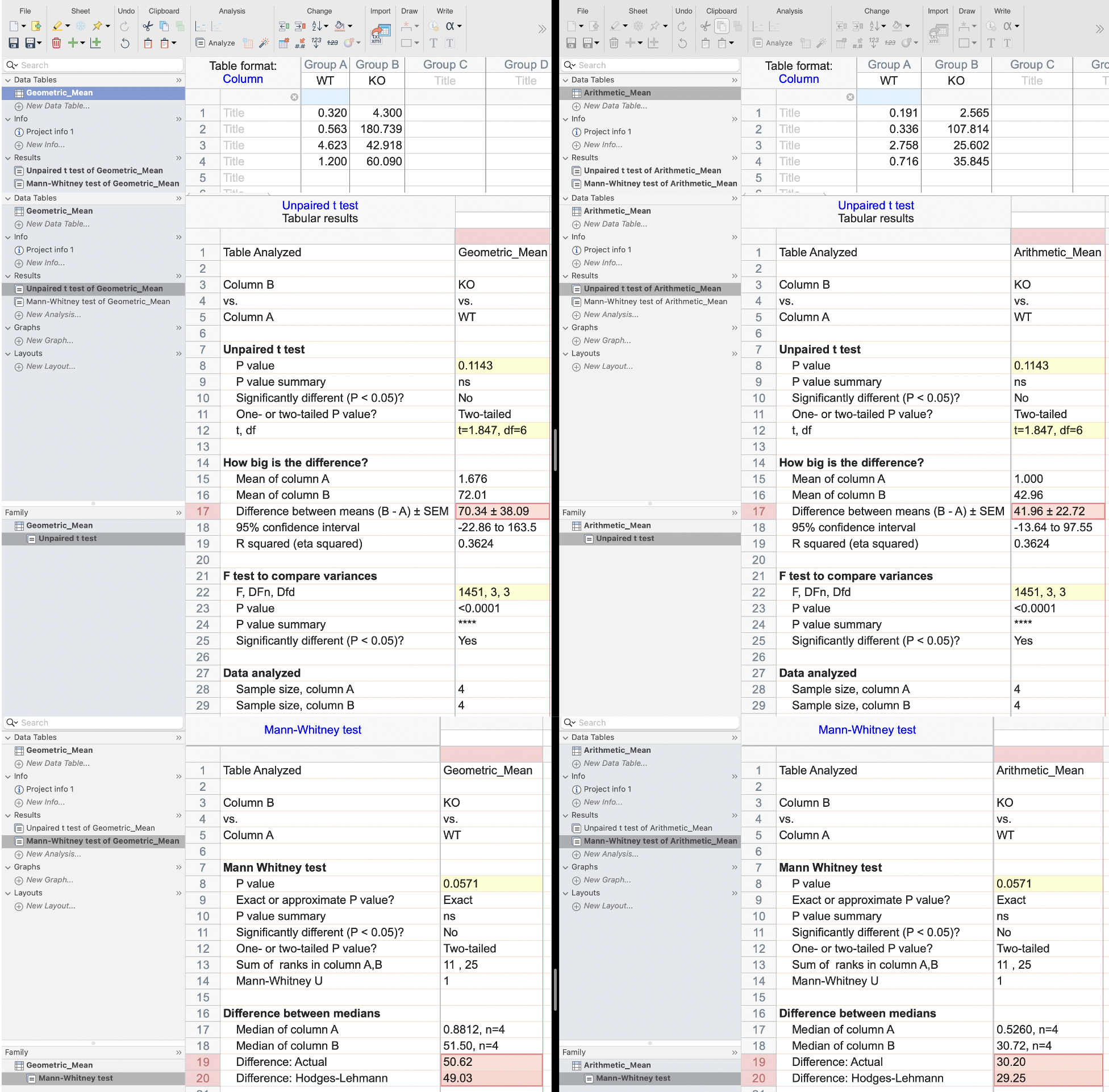Identical_qPCR_Results Figure 2. According to the GraphPad Prism output, the statistical parameters (e.g., P-value, F, t, etc.) remain exactly the same across different normalization strategies (GM_Calibrator_2DDCt.prism and AM_Calibrator_2DDCt.prism). However, the actual differences between groups (e.g., A–B) are not identical. This is why we focus on fold-change: since the ΔΔCt method is inherently based on relative quantification, the fold-change values remain unchanged under linear rescaling of the input data (see Figure 1 in this post).

4.4 Either is fine

Despite the mathematical nuances we’ve explored, real-world evidence supports the validity of both normalization strategies. In practical settings, the ΔΔCt method is rarely used for exact quantification. What researchers care about most is not whether the fold change is 3.4× or 3.7×, but rather whether the change is statistically significant and biologically meaningful. In this regard, the method has always been more semi-quantitative or directional than strictly quantitative.

Since the publication of Livak and Schmittgen’s 2001 paper, thousands of studies—including clinical trials and drug discovery pipelines—have applied $2^{-\Delta\Delta C_T}$ with mixed use of arithmetic and geometric normalizations. And guess what? It didn’t break science. Research conclusions still held. Drug candidates still moved forward. Diagnostic markers were still validated.

Why? Because the differences (e.g. scaled SD, etc.) introduced by using arithmetic vs. geometric mean for normalization is typically negligible—especially when your study design includes both technical and biological replicates. That’s because the SD of qPCR results is influenced far more by the properties of your system—including your instrument performance, qPCR reagents, genes’ sequences, and the biological heterogeneity of your organisms or cells —than by how you normalize your results. In other words, normalization method of $2^{-\Delta\Delta C_T}$ contributes little to your final error bars compared to these upstream sources of variability.

So if your control group’s mean isn’t exactly 1 after ΔΔCt normalization—and you’re tempted to “fix” it with an extra step—don’t worry. Whether you normalize to the geometric mean or rescale using the arithmetic mean, both approaches are mathematically defensible and empirically safe.

🧾 Final Summary: It’s Not About Being Perfect—It’s About Being Transparent

So, what did we learn?

Mathematically, normalizing $2^{-\Delta\Delta C_T}$ by the control group’s mean (arithmetic or geometric) yields equivalent results. This is not a hack—it’s a property of log-transformed data and the algebra of exponentiation.
The original ΔΔCt method, as proposed by Livak & Schmittgen (2001), implicitly uses the geometric mean (via the arithmetic mean of ΔCt) for defining the calibrator. Yet, it presents fold-change results using arithmetic mean in the linear space—justified by real-world variance considerations.
When you perform statistical tests on ΔΔCt values (which are in log space), the results—P-values, t-statistics, ANOVA F-ratios—do not change regardless of whether you apply secondary normalization or not.
Most importantly, the fold-change stays the same, and the differences in SD are minor, especially when your experiment includes proper biological and technical replication.

But here’s the key takeaway:

✅ Both methods are mathematically defensible and statistically safe—but only if you report clearly what you did.

Whether you use geometric or arithmetic normalization, whether your control group mean is exactly 1 or slightly off, what matters most is transparency. State your assumptions. Describe your normalization steps. Let readers see your workflow.

Because science doesn’t demand perfection—it demands reproducibility.

🎯 Bottom line:
The ΔΔCt method is robust. Your conclusions won’t fall apart because you chose one normalization method over another. But your credibility will always be stronger when your math—and your methods—are fully transparent.

— by WANG Ziyi GitHub Profile

References

If you found this helpful, feel free to comment, share, and follow for more. Your support encourages us to keep creating quality content.

PREVIOUSqPCR における ΔΔCt 法を使用する際に知っておくべきすべてのこと